ELECTRONIQUE 3D

L'ELECTRONIQUE FACILE ET AMUSANTE
Le filtre passe bas
Cliquer sur les images pour agrandir
- Le rôle d'un filtre est de laisser passer les fréquences utiles, et de supprimer les fréquences indésirables.
- Les filtres basses fréquences sont une association de résistances et capacités ou de selfs et capacités. Un filtre est dit actif quand des composants actifs (circuits intégrés ou transistors), jouent un rôle dans la constitution du filtre, ils autorisent une amplification, ce qui n'est pas le cas avec les filtres passifs.
- Il est souvent utile d'avoir recours aux filtres, que ce soit en basse fréquence ou autres (filtres audio). Il existe différents types de filtres.
- En prenant exemple de la voix humaine, on utilisera par exemple un filtre passe-bande allant de 300 Hz à 2500 Hz. Ceci étant défini, il convient de déterminer la pente du filtre.
- Les filtres basses fréquences sont une association de résistances et capacités ou de selfs et capacités. Un filtre est dit actif quand des composants actifs (circuits intégrés ou transistors), jouent un rôle dans la constitution du filtre, ils autorisent une amplification, ce qui n'est pas le cas avec les filtres passifs.
- Il est souvent utile d'avoir recours aux filtres, que ce soit en basse fréquence ou autres (filtres audio). Il existe différents types de filtres.
- Le filtre passe-bas- Par exemple, si l'on souhaite la mise en valeur d'une certaine bande de fréquence, comme la voix d'un enregistrement audio, on aura recours à un filtre passe-bande. Celui-ci éliminant les fréquences autres que celle correspondant à la voix et on pourra si l'on veut, amplifier cette bande de fréquence.
- Le filtre passe-haut
- Le filtre passe-bande
- Le filtre de coupe bande ou filtre de Notch
- En prenant exemple de la voix humaine, on utilisera par exemple un filtre passe-bande allant de 300 Hz à 2500 Hz. Ceci étant défini, il convient de déterminer la pente du filtre.
- Cette pente se définit en décibels par octaves. Pour se faire une idée du décibel ici et là. Le terme octave définit les fréquences multiples (facteur deux) et sous-multiples de la fréquence considérée. Par exemple, 1000 Hz, les octaves supérieures sont 2000 Hz, 4000 Hz, 8000 Hz, 16000 Hz. Les octaves inférieures sont 500 Hz, 250 Hz, 125 Hz etc.
- Cette pente se définie aussi par décades (facteur 10).
- Cette pente se définie aussi par décades (facteur 10).
Ordre des filtres:
Les filtres le plus souvent utilisés en basse fréquence vont de 6 à 24 dB.
6 dB par octave (20 dB décade) Filtre de 1° ordre12 dB par octave (40 dB décade)Filtre de 2° ordre18 dB par octave (60 dB décade) Filtre de 3° ordre24 dB par octave (80 dB décade) Filtre de 4° ordre30 dB par octave<(100 dB décade) Filtre de 5° ordre36 dB par octave (120 dB décade) Filtre de 6° ordre42 dB par octave (140 dB décade) Filtre de 7° ordre
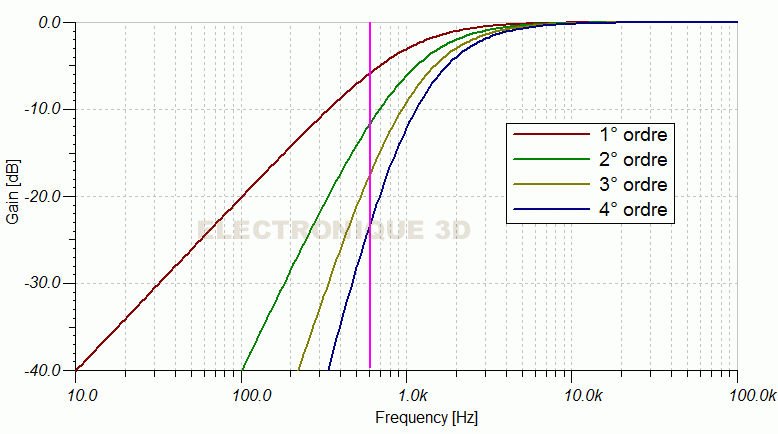
- On voit ci-dessus un filtre passe haut à une fréquence de coupure de 1000 Hz, la fréquence de coupure se définit à -3 dB. On voit également que l'ordre d'un filtre exprime son efficacité. Si l'on regarde l'atténuation de la fréquence de 500 Hz, celle-ci est de 6 dB pour un filtre de 1° ordre et de 24 dB pour un filtre de 4° ordre.
- Moins 3 dB correspond à quoi ?
- C'est une norme, cela correspond à la tension d'entrée divisée par 1,414 (racine 2), ce qui correspond à 70,7% du signal d'entré.
Atténuation en fonction des décibels.
|
3 dB par octave =1,41 6 dB par octave =1,99 12 dB par octave =3,98 18 dB par octave =7,94 20 dB par octave = 10 |
|
|
Quelques courbes de différents filtres:
- Courbes de réponse de filtres BF:
- Courbes de réponse de filtres BF:
Cliquer sur les images pour agrandir
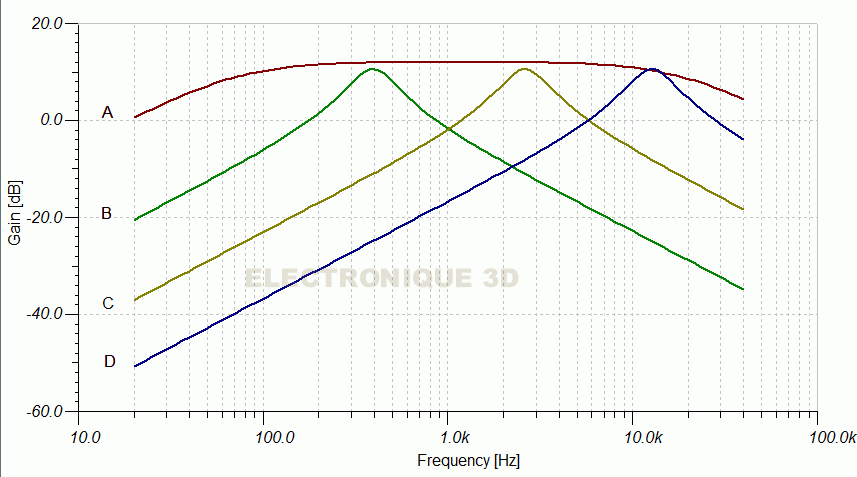
Figure 2 Courbe de réponse
Figure 3 Filtre passe-bas
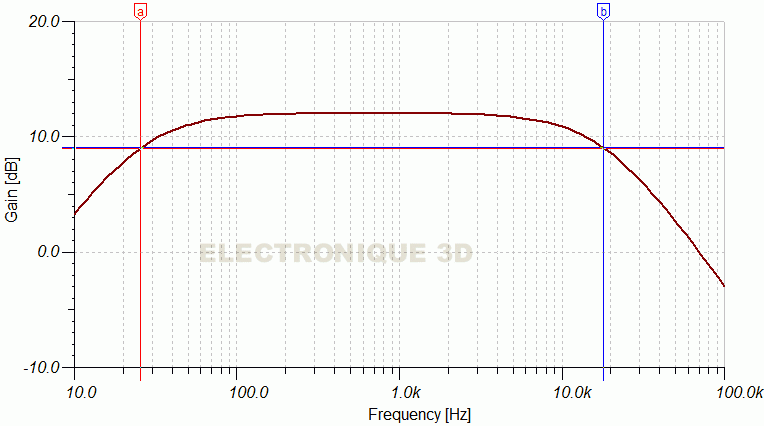
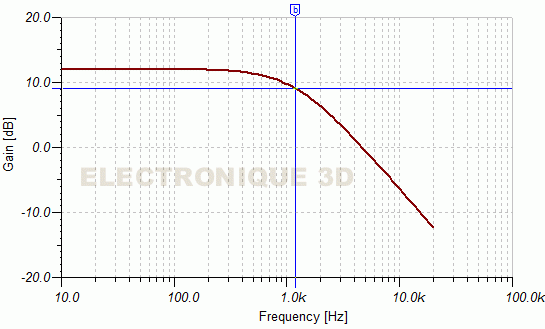
Figure 4 Filtre passe-haut
Figure 5 Filtre à bande étroite
- Figure 2 : Bande passante d'un amplificateur. Ce diagramme n'est pas un filtre, il montre la bande passante d'un amplificateur. Ici, le gain est de 16 dB et que sa bande passante va de 26 Hz à 18 Khz environ, la mesure se fait aussi à -3dB.
- Figure 3 : Filtre passe-bas. Fréquence de coupure Fc= 1Khz. Ce filtre laisse passer les signaux en deçà de la fréquence de coupure, seules les fréquences hautes sont atténuées.
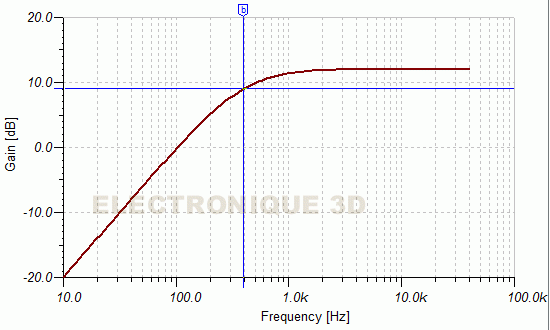
- Figure 4 : Filtre passe-haut. Fréquence de coupure Fc= 1Khz. c'est l'inverse du filtre passe bas, seules les fréquences basses sont atténuées.
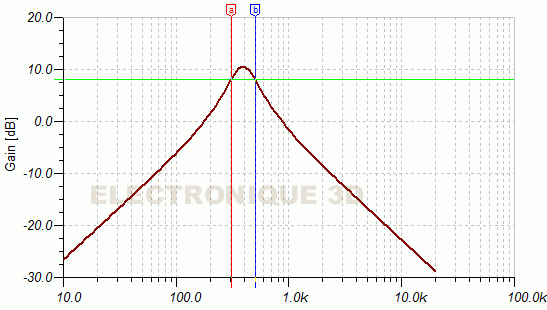
- Figure 5 : Filtre à bande étroite. Seule une petite largeur de bande est privilégiée.
- Le filtre passe-bas :
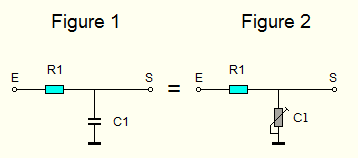
- Le filtre passe-bas le plus simple est l'association d'une résistance et d'une capacité. Figure 1 ci-dessous:
- Figure 3 : Filtre passe-bas. Fréquence de coupure Fc= 1Khz. Ce filtre laisse passer les signaux en deçà de la fréquence de coupure, seules les fréquences hautes sont atténuées.
- Figure 4 : Filtre passe-haut. Fréquence de coupure Fc= 1Khz. c'est l'inverse du filtre passe bas, seules les fréquences basses sont atténuées.
- Figure 5 : Filtre à bande étroite. Seule une petite largeur de bande est privilégiée.
- Le filtre passe-bas :
- Le filtre passe-bas le plus simple est l'association d'une résistance et d'une capacité. Figure 1 ci-dessous:
- Comment cela fonctionne-t'il ?
- Et bien, il faut considérer la réactance d'un condensateur C1, celle-ci varie en fonction de la fréquence du signal. Cette réactance est inversement proportionnelle à la fréquence, (elle diminue quand la fréquence augmente), on peut dire que le filtre se comporte comme un diviseur de tension, C1 étant en quelque sorte, une résistance variable commandée en fréquence. (Figure 2). Pour rappel, la réactance capacitive d'un condensateur (capacitance) = 1/ 2 pi (F*C).
La fréquence de coupure Fc du filtre est égale à 1/2pi (R*C), dans laquelle Fc est en Hz, R en ohm et C en farad. Comme il est laborieux de convertir des farads en NF, il est plus facile de prendre comme formule Fc = 159155/(R*C) avec Fc en Hz, R en K-ohms et C en NF. (1/2 pi= 0,159155).
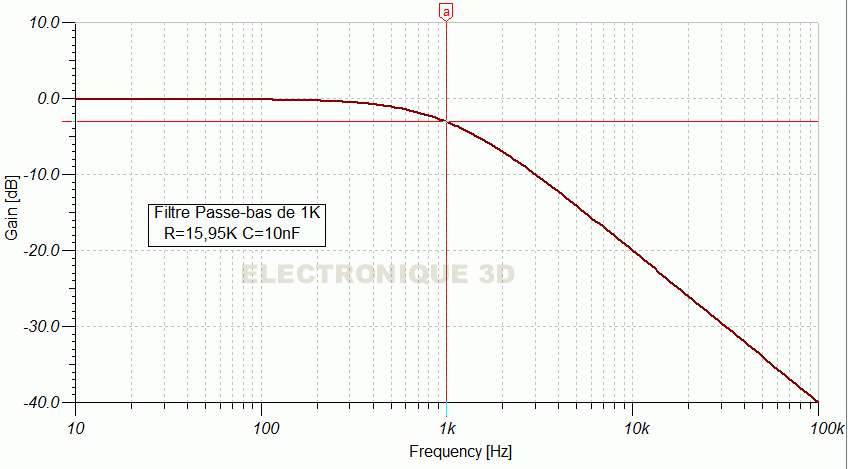
- Prenons un filtre passe-bas avec R1= 15 K, C1= 10 nF. Fc = 159155/(15*10)= 1061 Hz
- Oui, mais moi, je veux un filtre passe-bas de 1000 Hz...
- Si tu veux un filtre passe-bas de 1000Hz, de la formule citée plus haut en découlent deux autres. C1 = 159155/ (R1*Fc), R1= 159155/ (C1*Fc).
- Pour un filtre de 1000 Hz, R1= 159155/(10nF*1000Hz)= 15,91K
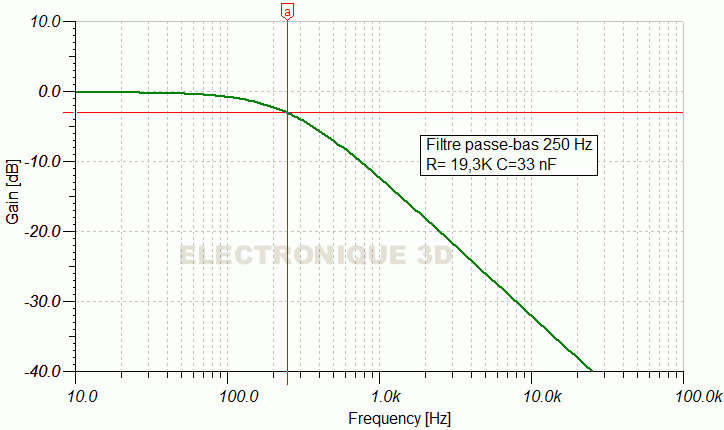
- Deuxième exemple : Calcul d'un filtre passe-bas avec une fréquence de coupure Fc de 250 Hz.
Calcul de R1 en ayant un condensateur de 33 nF (valeur a priori), R1= 159155/(33*250)= 19,30 K.
- Le filtre passif 1000 Hz et 250 Hz sur simulateur :
- Et bien, il faut considérer la réactance d'un condensateur C1, celle-ci varie en fonction de la fréquence du signal. Cette réactance est inversement proportionnelle à la fréquence, (elle diminue quand la fréquence augmente), on peut dire que le filtre se comporte comme un diviseur de tension, C1 étant en quelque sorte, une résistance variable commandée en fréquence. (Figure 2). Pour rappel, la réactance capacitive d'un condensateur (capacitance) = 1/ 2 pi (F*C).
La fréquence de coupure Fc du filtre est égale à 1/2pi (R*C), dans laquelle Fc est en Hz, R en ohm et C en farad. Comme il est laborieux de convertir des farads en NF, il est plus facile de prendre comme formule Fc = 159155/(R*C) avec Fc en Hz, R en K-ohms et C en NF. (1/2 pi= 0,159155).
- Prenons un filtre passe-bas avec R1= 15 K, C1= 10 nF. Fc = 159155/(15*10)= 1061 Hz
- Oui, mais moi, je veux un filtre passe-bas de 1000 Hz...
- Si tu veux un filtre passe-bas de 1000Hz, de la formule citée plus haut en découlent deux autres. C1 = 159155/ (R1*Fc), R1= 159155/ (C1*Fc).
- Pour un filtre de 1000 Hz, R1= 159155/(10nF*1000Hz)= 15,91K
- Deuxième exemple : Calcul d'un filtre passe-bas avec une fréquence de coupure Fc de 250 Hz.
Calcul de R1 en ayant un condensateur de 33 nF (valeur a priori), R1= 159155/(33*250)= 19,30 K.
- Le filtre passif 1000 Hz et 250 Hz sur simulateur :
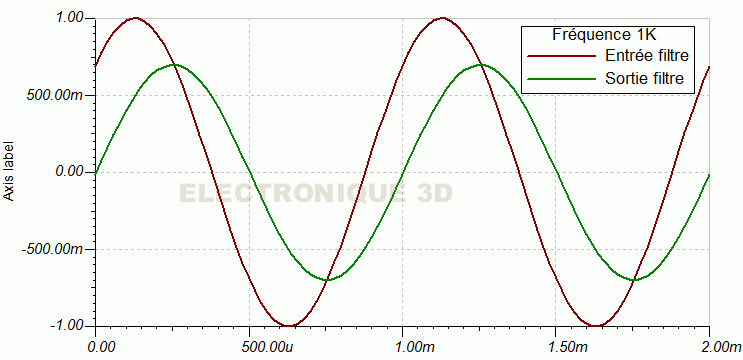
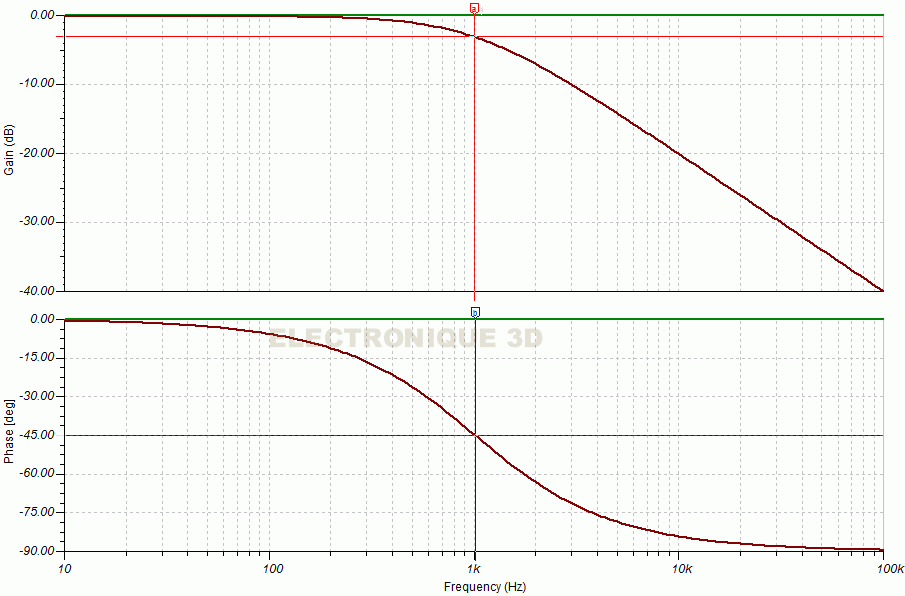
Cliquer pour agrandir
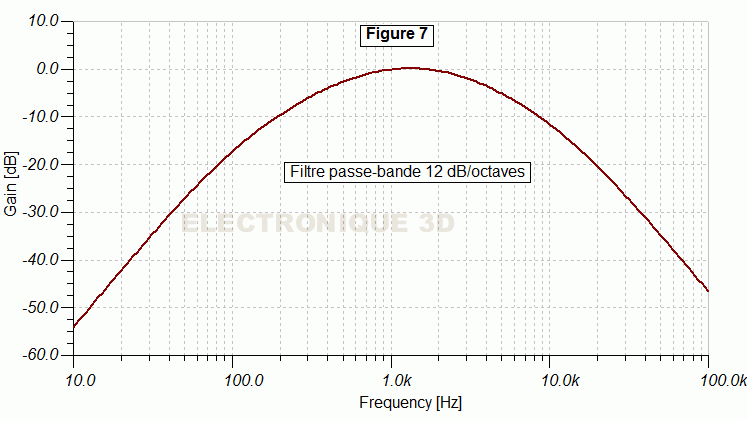
- Nicolas, on vient de voir un filtre de 6 dB par octave, si on veut le rendre plus sélectif, il est possible par exemple de mettre en série deux cellules R-C, ce qui donne un filtre de 12 décibels/octaves.
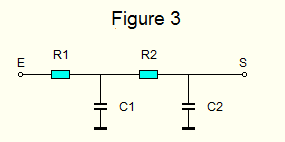
- La fréquence de coupure est, Fc (Hz)= 1/2pi ( √ R1*C1*R2*C2), avec R= Ohm et C en Farad. Soit pour le filtre de 1000 Hz, R1-R2= 15,91 K, C1-C2= 10nF, en simplifiant la formule comme plus haut,
Fc= 159155/ (√ 15,91*10*15,91*10)= 1000 Hz.
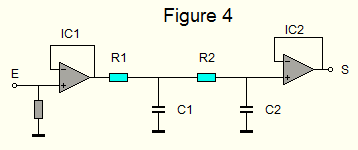
- Tel qu'il est en figure 3, le filtre n'est guère utilisable, et effet la fréquence de coupure calculée est tributaire de l'impédance du circuit connecté à l'entrée du filtre et à sa sortie, c'est pourquoi il est conseillé de précéder le filtre d'un adaptateur d'impédance (IC1-IC2), ainsi qu' à la sortie, Figure 4.
- Le filtre passe-haut :
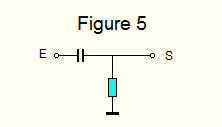
- Le filtre passe-haut se calcule comme le filtre passe bas. Il faut juste inverser les composants, Figure 5.
Fc= 159155/ (√ 15,91*10*15,91*10)= 1000 Hz.
- Tel qu'il est en figure 3, le filtre n'est guère utilisable, et effet la fréquence de coupure calculée est tributaire de l'impédance du circuit connecté à l'entrée du filtre et à sa sortie, c'est pourquoi il est conseillé de précéder le filtre d'un adaptateur d'impédance (IC1-IC2), ainsi qu' à la sortie, Figure 4.
- Le filtre passe-haut :
- Le filtre passe-haut se calcule comme le filtre passe bas. Il faut juste inverser les composants, Figure 5.
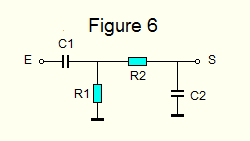
- Filtre passe-bande :
- Un filtre passe-bande est réalisé en mettant en série un filtre passe-haut C1-R1, suivi d'un filtre passe-bas R2-C2. Figure 6. La aussi, il est conseillé de précéder le filtre d'un adaptateur d'impédance (IC1-IC2), ainsi qu' à la sortie, Figure 4.
- Les filtres actifs :
- Les filtres passifs abordés plus haut sont simples à mettre en œuvre, mais à vrai dire n'apporte pas grand chose, car il est souvent utile d'avoir des filtres plus sélectifs. On fait alors appel à des filtres actifs.
- Les filtres actifs comportent plusieurs catégories. Les plus connus sont les filtres de Butterworth, Bessel, Tchébyscheff.
En basse fréquence, notamment en Hi-Fi, on utilise généralement le filtre de Butterworth. Ce filtre ayant une réponse amplitude-fréquence la plus plate.
Filtres actifs Butterworth
- Filtre actif passe-bas 1000Hz - 12 dB/octave - Butterworth
- Voici les schémas d'un filtre actif passe-bas et passe-haut de 12dB/octave. L'amplificateur opérationnel est monté en suiveur de tension, il n'y a donc pas de gain. Figure 8.
- Un filtre passe-bande est réalisé en mettant en série un filtre passe-haut C1-R1, suivi d'un filtre passe-bas R2-C2. Figure 6. La aussi, il est conseillé de précéder le filtre d'un adaptateur d'impédance (IC1-IC2), ainsi qu' à la sortie, Figure 4.
- Les filtres actifs :
- Les filtres passifs abordés plus haut sont simples à mettre en œuvre, mais à vrai dire n'apporte pas grand chose, car il est souvent utile d'avoir des filtres plus sélectifs. On fait alors appel à des filtres actifs.
- Les filtres actifs comportent plusieurs catégories. Les plus connus sont les filtres de Butterworth, Bessel, Tchébyscheff.
En basse fréquence, notamment en Hi-Fi, on utilise généralement le filtre de Butterworth. Ce filtre ayant une réponse amplitude-fréquence la plus plate.
Filtres actifs Butterworth
- Filtre actif passe-bas 1000Hz - 12 dB/octave - Butterworth
- Voici les schémas d'un filtre actif passe-bas et passe-haut de 12dB/octave. L'amplificateur opérationnel est monté en suiveur de tension, il n'y a donc pas de gain. Figure 8.
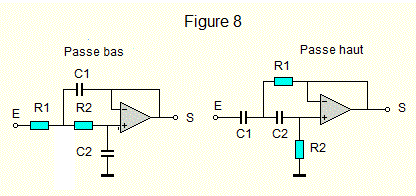
Filtre de Butterworth passe-haut et passe-bas
- Tu remarques Nicolas, que comme vu plus haut, les résistances et capacités sont inversées entre passe-haut et passe-bas.
- Pour comprendre rapidement la suite, tu considères que R0 = R1=R2 et C0= C1-C2. Ensuite, on pose arbitrairement la valeur de R0, sachant que cette valeur doit être comprise entre 4,7K et 10K. Pour me simplifier la vie, je prends R0=10K, R1 et R2 auront donc cette valeur.
La fréquence de coupure du filtre est égal à Fc = 159155/(R0*C0) avec RO en K-Ohms et C0 en nF.
- Jusque-là, cela va, tu piges !
OK!
De la formule Fc = 159155/R0*C0 on déduit que C0= 159155/(R0*Fc), ainsi pour un filtre passe-bas de 1000Hz, C0= 159155/(10k*1000Hz)= 15,9 nF. De C0 va découler C1 et C2, en prenant deux constantes qui définissent la classe du filtre, pour un filtre de Butterworth. C1 sera égal à C0*1,414 et C2 sera égal à C0*0,707. Ainsi C1= 22,5 nF, C2= 11,24 nF.
- Tu vois donc que cela n'est pas très compliqué...
Récapitulation :
On veut un filtre passe bas avec une fréquence de coupure Fc de 1000 Hz.
On choisit arbitrairement R0 (qui doit être compris en 4,7k et 10K). La valeur choisie est 10K.
La fréquence de coupure Fc= 159155/(R0*C0) d'où C0= 159155/(R0*Fc), soit C0= 159155/(10k*1000Hz)= 15,9 nF.
Ainsi R1=R2= 10K, C1= C0*1,414= 22,5 nF, C2= C0*0,707= 11,2 nF
- Allure du filtre ainsi calculé :
- Pour comprendre rapidement la suite, tu considères que R0 = R1=R2 et C0= C1-C2. Ensuite, on pose arbitrairement la valeur de R0, sachant que cette valeur doit être comprise entre 4,7K et 10K. Pour me simplifier la vie, je prends R0=10K, R1 et R2 auront donc cette valeur.
La fréquence de coupure du filtre est égal à Fc = 159155/(R0*C0) avec RO en K-Ohms et C0 en nF.
- Jusque-là, cela va, tu piges !
OK!
De la formule Fc = 159155/R0*C0 on déduit que C0= 159155/(R0*Fc), ainsi pour un filtre passe-bas de 1000Hz, C0= 159155/(10k*1000Hz)= 15,9 nF. De C0 va découler C1 et C2, en prenant deux constantes qui définissent la classe du filtre, pour un filtre de Butterworth. C1 sera égal à C0*1,414 et C2 sera égal à C0*0,707. Ainsi C1= 22,5 nF, C2= 11,24 nF.
- Tu vois donc que cela n'est pas très compliqué...
Récapitulation :
On veut un filtre passe bas avec une fréquence de coupure Fc de 1000 Hz.
On choisit arbitrairement R0 (qui doit être compris en 4,7k et 10K). La valeur choisie est 10K.
La fréquence de coupure Fc= 159155/(R0*C0) d'où C0= 159155/(R0*Fc), soit C0= 159155/(10k*1000Hz)= 15,9 nF.
Ainsi R1=R2= 10K, C1= C0*1,414= 22,5 nF, C2= C0*0,707= 11,2 nF
- Allure du filtre ainsi calculé :
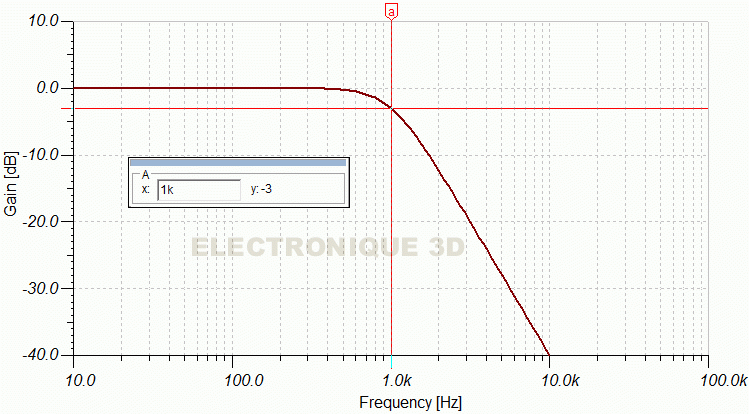
Filtre passe-bas 12 dB/octave_ R1=R2=10K C1=22,5nF_C2=11,24nF
- Tu vois sur simulateur, que la fréquence de coupure Fc à -3 dB= 1000Hz, et que le filtre n'apporte aucun gain.
- Filtre actif passe-haut 1000Hz - 12 dB/octave - Butterworth: Figure 8
- Tout se passe comme le filtre passe bas, sauf que ce sont les condensateurs qui sont choisis arbitrairement. Je prends C0= C1-C2= 10nF. Les deux constantes sont les mêmes, et comme vu plus haut C0 étant égal à 159155/(R0*Fc), alors RO= 159155/(C0*Fc).
- R0= 159155/(10nF*1000Hz)= 15,9K.
- R1= 15,9/1,414= 11,24K
- R2= 15,9/0,707= 22,48K
- Filtre actif passe-haut 1000Hz - 12 dB/octave - Butterworth: Figure 8
- Tout se passe comme le filtre passe bas, sauf que ce sont les condensateurs qui sont choisis arbitrairement. Je prends C0= C1-C2= 10nF. Les deux constantes sont les mêmes, et comme vu plus haut C0 étant égal à 159155/(R0*Fc), alors RO= 159155/(C0*Fc).
- R0= 159155/(10nF*1000Hz)= 15,9K.
- R1= 15,9/1,414= 11,24K
- R2= 15,9/0,707= 22,48K
Filtre Butterworth passe-haut 1000 Hz 12 dB/octave
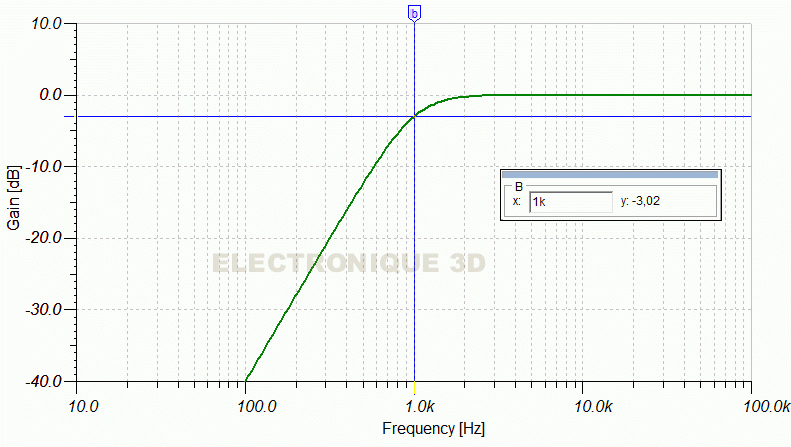
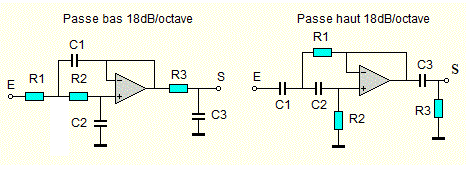
- Filtre passe-bas 1000 Hz - 18dB/octave.
- Comme pour les filtres passifs, si l'on adjoint un réseau R-C de 6dB/octave en sortie, on obtient un filtre de 18dB/octave.
- Comme pour les filtres passifs, si l'on adjoint un réseau R-C de 6dB/octave en sortie, on obtient un filtre de 18dB/octave.
C0 = 159155/R0*Fc, R0= 159155/C0*Fc.
- Reprendre les formules du filtre passe-bas 12dB, mais les constantes changes.
- R0= R1=R2=R3 et C0= C1-C2-C3.
- R0=R1=R2=R3= 10K (valeur arbitrairement choisie). C0= 159155/(10k*1000Hz)= 15,9 nF
- C1= CO*1,999= 31,6 nF
- C2= C0*0,5= 7,95 nF
- C3= C0= 15,9 nF
- Filtre passe-haut 1000 Hz - 18dB/octave :
- Reprendre les formule du filtre passe-haut 12dB, mais les constantes changes.
- C0= C1-C2-C3= 10nF (valeur arbitrairement choisie). R0= 159155/(10nF*1000Hz)= 15,9 K
- R1= R0/1,99= 7,98 K
- R2= R0/0,5= 31,8K
- R3= R0= 15,9K.
- Filtre passe-bas 24 dB/octave :
- En alignant deux filtres de 12dB/octave on obtient un filtre 24 dB/octave.
- Reprendre les formules du filtre passe-bas 12dB, mais les constantes changes.
- R0= R1=R2=R3 et C0= C1-C2-C3.
- R0=R1=R2=R3= 10K (valeur arbitrairement choisie). C0= 159155/(10k*1000Hz)= 15,9 nF
- C1= CO*1,999= 31,6 nF
- C2= C0*0,5= 7,95 nF
- C3= C0= 15,9 nF
- Filtre passe-haut 1000 Hz - 18dB/octave :
- Reprendre les formule du filtre passe-haut 12dB, mais les constantes changes.
- C0= C1-C2-C3= 10nF (valeur arbitrairement choisie). R0= 159155/(10nF*1000Hz)= 15,9 K
- R1= R0/1,99= 7,98 K
- R2= R0/0,5= 31,8K
- R3= R0= 15,9K.
- Filtre passe-bas 24 dB/octave :
- En alignant deux filtres de 12dB/octave on obtient un filtre 24 dB/octave.
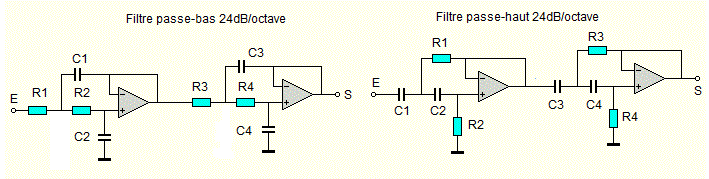
- On continue sur le même principe, les constantes changes,
- R0= R1=R2=R3=R4 et C0= C1-C2-C3-C4.
- R0=R1=R2=R3= 10K (valeur arbitrairement choisie). C0= 159155/(10k*1000Hz)= 15,9 nF
- C1= C0*1.0824= 17,17 nF
- C2= C0*0,9239= 14,69 nF
- C3= C0*2,6130= 41,5 nF
- C4= C0*0,3827= 6,08 nF
- Filtre passe-haut 24 dB/octave :
C0= C1-C2-C3=C4= 10nF (valeur arbitrairement choisie). R0= 159155/(10nF*1000Hz)= 15,9 nF
- R1= R0*0,9239= 14,7K
- R2= R0*1,0824= 17,21k
- R3= R0*0,3827= 6k
- R4= R0*2,8290= 41,5k.
- Il est évident qu'il faudra approcher au plus près la valeur des résistances et capacités de la valeur théorique. Comment obtenir des condensateurs de précision voir sur cette page.
- R0= R1=R2=R3=R4 et C0= C1-C2-C3-C4.
- R0=R1=R2=R3= 10K (valeur arbitrairement choisie). C0= 159155/(10k*1000Hz)= 15,9 nF
- C1= C0*1.0824= 17,17 nF
- C2= C0*0,9239= 14,69 nF
- C3= C0*2,6130= 41,5 nF
- C4= C0*0,3827= 6,08 nF
- Filtre passe-haut 24 dB/octave :
C0= C1-C2-C3=C4= 10nF (valeur arbitrairement choisie). R0= 159155/(10nF*1000Hz)= 15,9 nF
- R1= R0*0,9239= 14,7K
- R2= R0*1,0824= 17,21k
- R3= R0*0,3827= 6k
- R4= R0*2,8290= 41,5k.
- Il est évident qu'il faudra approcher au plus près la valeur des résistances et capacités de la valeur théorique. Comment obtenir des condensateurs de précision voir sur cette page.
- Pour tous ces filtres actifs, la tension d'alimentation des AOP est symétrique.
Recherche sur le site
Recherche sur le web, axée sur l'électronique